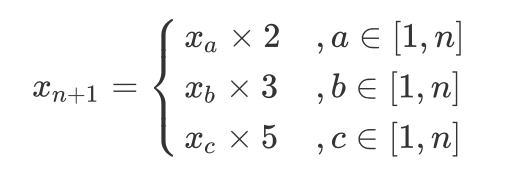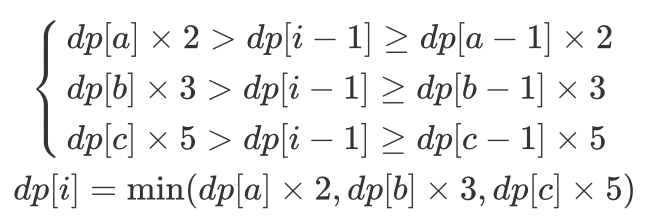题目信息

  • 题目：剑指 Offer 49. 丑数

  • 时间： 2020-08-23

  • 题目链接：Leetcode

  • tag：动态规划 小根堆

  • 难易程度：中等

  • 题目描述：

    我们把只包含质因子 2、3 和 5 的数称作丑数（Ugly Number）。求按从小到大的顺序的第 n 个丑数。

示例:

1
2
3
输入: n = 10
输出: 12
解释: 1, 2, 3, 4, 5, 6, 8, 9, 10, 12 是前 10 个丑数。

注意

1
2
1. 1是丑数
2. n < 1690

解题思路

本题难点

丑数的定义以及查找的方式

具体思路

丑数只包含因子 2,3,5 ，因此有 “丑数 = 某较小丑数 × 某因子” （例如：10=5×2）

设已知长度为 n 的丑数序列 x1,x2,⋯,xn ，求第 n+1 个丑数 xn+1 。根根据递推性质，丑数 x n+1 只可能是以下三种情况其中之一（索引 a,b,c 为未知数）：

xn+1={xa×2,a∈[1,n]xb×3,b∈[1,n]xc×5,c∈[1,n]x_{n+1}=\left\{\begin{array}{ll} x_{a} \times 2 & , a \in[1, n] \\ x_{b} \times 3 & , b \in[1, n] \\ x_{c} \times 5 & , c \in[1, n] \end{array}\right.

NzutrF.png

由于 x n+1 是 最接近 x n的丑数，因此索引 a,b,c 需满足以下条件：

{xa×2>xn≥xa−1×2, 即 xa 为首个乘以2后大于 xn 的丑数 xb×3>xn≥xb−1×3, 即 xb 为首个乘以3后大于 xn 的丑数 xc×5>xn≥xc−1×5, 即 xc 为首个乘以5后大于 xn 的丑数 \left\{\begin{array}{ll} x_{a} \times 2>x_{n} \geq x_{a-1} \times 2 & , \text { 即 } x_{a} \text { 为首个乘以2后大于 } x_{n} \text { 的丑数 } \\ x_{b} \times 3>x_{n} \geq x_{b-1} \times 3 & , \text { 即 } x_{b} \text { 为首个乘以3后大于 } x_{n} \text { 的丑数 } \\ x_{c} \times 5>x_{n} \geq x_{c-1} \times 5 & , \text { 即 } x_{c} \text { 为首个乘以5后大于 } x_{n} \text { 的丑数 } \end{array}\right.

Nzur26.png

若索引 a,b,c 满足以上条件，则可使用递推公式计算下个丑数 xn+1 ，其为三种情况中的最小值，

即：xn+1=min(xa × 2, xb × 3, xc × 5)

动态规划思想：

  • 状态定义：设动态规划列表 dp ，dp[i] 代表第 i+1 个丑数。

  • 转移方程：每轮计算 dp[i] 后，需要更新索引 a,b,c 的值，使其始终满足方程条件。实现方法：分别独立判断 dp[i] 和 dp[a]×2 , dp[b]×3 , dp[c]×5 的大小关系，若相等则将对应索引 a,b,c 加 1 。

    {dp[a]×2>dp[i−1]≥dp[a−1]×2dp[b]×3>dp[i−1]≥dp[b−1]×3dp[c]×5>dp[i−1]≥dp[c−1]×5dp[i]=min⁡(dp[a]×2,dp[b]×3,dp[c]×5)\begin{array}{c} \left\{\begin{array}{l} d p[a] \times 2>d p[i-1] \geq d p[a-1] \times 2 \\ d p[b] \times 3>d p[i-1] \geq d p[b-1] \times 3 \\ d p[c] \times 5>d p[i-1] \geq d p[c-1] \times 5 \end{array}\right. \\ d p[i]=\min (d p[a] \times 2, d p[b] \times 3, d p[c] \times 5) \end{array}

NzucrD.png

注意: dp[0]=1，第一个丑数为 1 ；

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
    public int nthUglyNumber(int n) {
        int a = 0, b = 0, c = 0;
        int[] dp = new int[n];
      //第一个丑数为 1
        dp[0] = 1;
        for(int i = 1 ; i < n ; i++){
            int n2 = 2 * dp[a];
            int n3 = 3 * dp[b];
            int n5 = 5 * dp[c];
            dp[i] = Math.min(Math.min(n2,n3),n5);
            if(dp[i] == n2){
                a++;
            }
            if(dp[i] == n3){
                b++;
            }
            if(dp[i] == n5){
                c++;
            }
        }
        return dp[n-1];
    }
}

复杂度分析：

  • 时间复杂度 O(N) ： 其中 N=n ，动态规划需遍历计算 dp列表。
  • 空间复杂度 O(N) ： 长度为 N 的 dp 列表使用 O(N)的额外空间。

其他优秀解答

解题思路

小根堆，要去找第n个丑数，首先想到的就是一个个去生成。uglyNum=2^x ∗3^y ∗5^z ，由 1 生成了 2、3、5 ，接着 2、3、5 利用前面公式继续生成。生成过程是先放小的，并且我们需要去重，去重就需要用到 set

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution {
    public int nthUglyNumber(int n) {
      //小根堆
        PriorityQueue<Long> pq = new PriorityQueue<>();
        Set<Long> s = new HashSet<>();
        //初始化,放进堆和set，发现1要开Long数组才可以
        long[] primes = new long[]{2, 3, 5};
        for (long prime : primes) {
            pq.offer(prime);
            s.add(prime);
        }
        long num = 1;
        for (int i = 1; i < n; i++) {
            num = pq.poll();
            //遍历三个因子
            for (int j = 0; j < 3; j++) {
                if (!s.contains(num * primes[j])) {
                    pq.offer(num * primes[j]);
                    s.add(num * primes[j]);
                }
            }
        }
        return (int) num;
    }
}